边界层

实际流体流经固体壁面时，在紧靠壁面附近形成的具有横向流速梯度的流体层。在实际流体的流动中，由于黏滞性对流动的影响，紧贴壁面的流体质点黏附于壁面上，水流与固体壁面的相对速度为零，称无滑移条件。沿壁面法线方向向外，水流流速逐层增大，直到接近势流的自由流速，从而在壁面附近形成一个流速减慢了的沿法线方向流速梯度较大的区域。普朗特（L.Prandtl）把这层流体称为边界层。对于边界层外部的流动则可忽略黏滞性的影响，而近似地作为理想流体流动处理。这样就把整个水流运动分为边界层和势流区，为应用数学方法解决流动问题开辟了道路。边界层理论由普朗特在1904年提出，它是水流阻力和水头损失计算的理论基础。近百年来，边界层理论得到很大的发展，促进了航空、航天、化工、365bet中国大陆网址_365bet官网的微博_正规365彩票平台app下载、航海等很多工程领域的进步。

实用上边界层厚度指由壁面到流速为0.99U₀处的厚度（U₀为势流流速），以δ表示。边界层厚度与流动的雷诺数、绕流物体的形状、壁面粗糙度、自由流的状态等有关。由于确定边界层上边界具有一定的任意性，故又定义以下几种厚度：

位移厚度

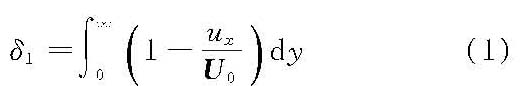
动量损失厚度

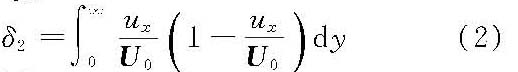
能量损失厚度

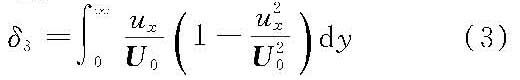
式中，u_x为边界层内y点的纵向流速。

边界层厚度是沿程发展的，而且随边界层内的流动型态（层流，紊流）的不同，其发展规律也不同（见图）。

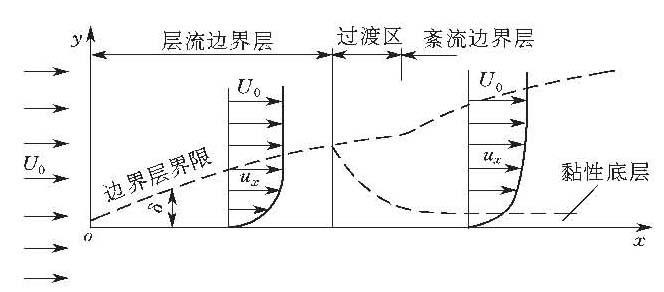
边界层的沿程发展示意图

边界层微分方程 纳维—斯托克斯方程在边界层的特定情况（δ/x＜＜1）下，进行量级分析而化简可分别得到边界层微分方程与连续方程如下：

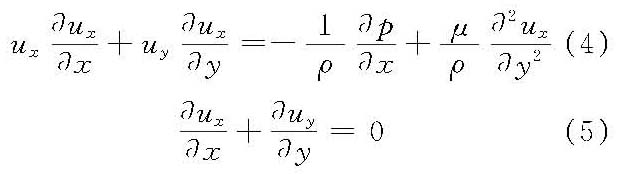
式中，u_y为沿壁面法向y的流速；p为液体压强；μ为动力黏滞系数；ρ为流体密度。

通常边界条件为

y=0; u_x=0; u_y=0

y=∞; u_x=U₀

对边界层微分方程沿y向积分而得边界层动量积分方程如下：

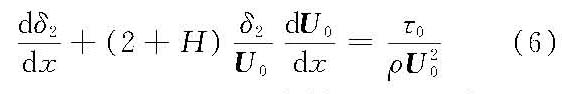
式中，H=δ₁/δ₂为形状参数；τ₀为壁面切应力。

具有自由水面的明渠水流流经固体壁面而形成明流边界层。在365bet中国大陆网址_365bet官网的微博_正规365彩票平台app下载工程中很多高速水流问题，如水流掺气，压强脉动，空化与空蚀，水头损失等都与明流边界层的特性有密切关系。