|
表述液体运动中能量守恒与转化规律的基本方程式。在不可压缩液体恒定流动中,沿流线对欧拉方程进行积分,可得到伯努利积分:w-(p/ρ)-(u2/2)=C,即在同一条流线上各质点的[w-(p/ρ)-(u2/2)]值是一个常数,但不同流线可能有各自的常数,彼此并不互等。 如果质量力只是重力,则力势函数w=-gz,伯努利积分可写为z+(p/γ)+(u2/2g)=C。式中,γ=ρg为流体的容重。 对同一元流上的任意两个断面1—1和2—2(图1)来说,则可写成
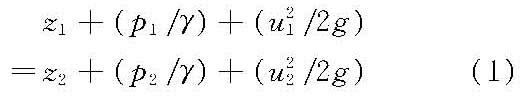
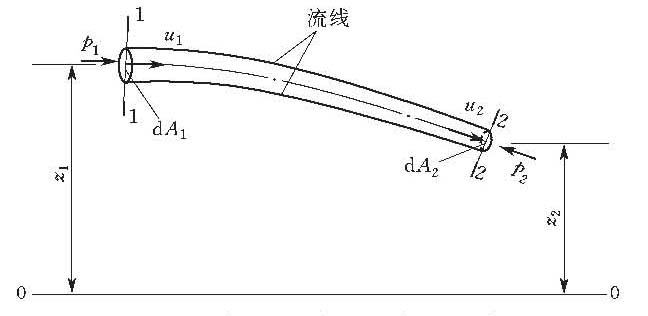
图1 恒定元流伯努利方程示意图
式中,z为单位重量液体所具有的位能;p/γ为单位重量液体所具有的压能;u2/2g为单位重量液体所具有的动能,其中下标1和2对应于元流断面1—1和2—2。 式(1)就是理想流体的能量方程式。这个方程式首先由伯努利(D.I. Bernoulli)于1738年提出,故称为伯努利方程。它说明,理想液体恒定流动中单位重量液体具有的总机械能在它所流经的任意位置上均保持不变,但其位能、压能和动能间则可以相互转换。因此,伯努利方程式实质上就是能量转化与守恒定律在液体运动中的特殊表达形式。 由于实际液体具有黏滞性,在流动过程中总要消耗一部分能量来克服摩擦阻力而作功,因此实际液体沿流动方向总能量逐渐减少。令单位重量液体从断面1—1至断面2—2所损失的能量为h′w,则实际液体恒定元流的伯努利方程为
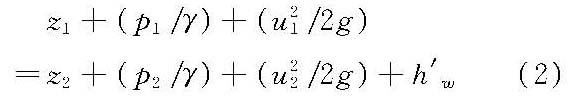
由无数元流所组成的整股水流叫做总流。实际液体恒定总流的伯努利方程为
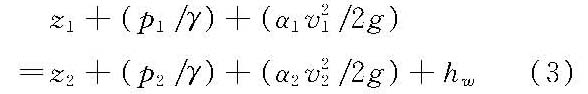
式(3)中的下标1和2分别代表所选总流的两个渐变流断面(图2)。在实际液流中,当流线之间的夹角很小而流线接近于平行,且流线曲率半径很大而流线接近直线时,这种液流称为渐变流。在渐变流中截取的过流断面称为渐变流断面。在恒定渐变流中同一个过流断面上z1+(p/γ)=C,C为常数。
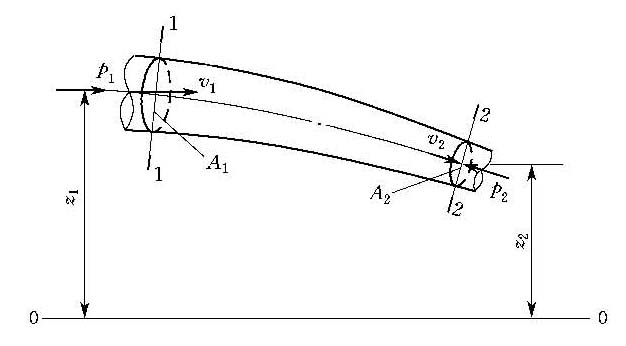
图2 恒定总流的伯努利方程式示意图
式(3)中,z1+(p1/γ),z2+(p2/γ)分别为断面1—1和断面2—2质点的单位重量液体的势能;v1、v2分别为断面1—1和2—2的平均流速;
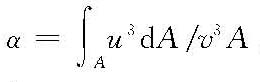
,为动能修正系数;hw为总流从断面1—1流至断面2—2的流动过程中单位重量液体所损耗的机械能的平均值。
式(3)是在一定的条件下推导出来的,应用时要注意以下几点:①液体是不可压缩的,流动是恒定的;②作用在液体上的质量力只有重力;③所选两个过流断面须是渐变流断面(两断面间可以是急变流);④前后两个过流断面是指同一股总流,即总流的流量沿程不变;⑤两个过流断面间除了水头损失hw外,无其他机械能的输入或输出。 在解决实际问题时,常常会遇到两断面间有流量分出或汇入,或存在其他机械能的输入或输出等情况,致使上述条件④或⑤得不到满足。此时,应根据具体情况对式(3)进行适当的修改和补充。
|

