层流边界层

流动形态为层流的边界层。层流边界层一般发生在绕流物体的上游部分，其微分方程是非线性偏微分方程组。早期对层流边界层问题的求解，常是找出无因次的组合自变量如η～y/δ，称为相似变量。y为壁面法线方向的坐标值，δ为边界层厚度。从而把偏微分方程化为常微分方程，并通过引入流函数（φ），把二维层流边界层偏微分方程组进一步化为一个常微分方程式，再用级数法求解。这种方法成功地解决了绕平板流动、绕楔形体流动、圆柱绕流等问题。随着电子计算机的广泛应用，已能使用有限差分法或有限单元法直接求得数值解。

1908年，布莱修斯（H. Blasius）得到平板层流边界层的精确解，其结果为

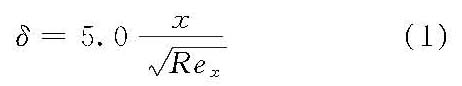
式中，Re_x=U₀x/ν为边界层水流雷诺数；U₀为来流速度；x为沿程坐标值；ν为运动黏滞系数。

平板层流摩擦阻力的有关系数为

切应力系数

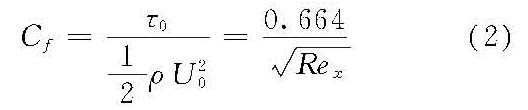
阻力系数

式中，b为板宽；l为板长；D为板一侧阻力；Re_l=U₀l/ν。

层流边界层还可应用边界层动量方程求得近似解。计算中首先假设一个流速分布函数，使之满足边界条件，从而可求出边界层厚度，切应力及阻力系数等数值。

边界层内的流动随着边界层雷诺数（Re）的增加，层流将失去稳定性而转变为紊流，形成紊流边界层。层流到紊流的转变也受到一些其他因素的影响，如自由流紊流度、纵向压力梯度、固体壁面的粗糙度、壁面曲率、边界层的吸出或吹入等。平板层流边界层转变为紊流边界层的临界雷诺数为3×10⁵＜（Re_x）_c＜3×10⁶。