沉速

泥沙在水中均匀下沉的速度。

球体在静水中受重力（W）作用而下沉。

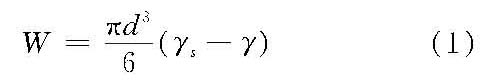
式中，d为球体直径；γ_s为球体单位体积重；γ为水的单位体积重。

泥沙在下沉过程中又受到水流阻力（F）的作用。

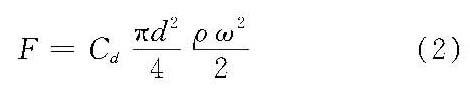
式中，ω为球体沉速；ρ为水密度；C_d为阻力系数。

下沉开始，重力大于阻力，球体呈加速运动，经过一段距离后，阻力与重力相等，球体以均匀速度下沉，此时的下沉速度即为球体的沉速，据此可以导出球体沉速公式

式中，g为重力加速度；C_d为阻力系数，是颗粒雷诺数（Re_d）的函数，Re_d=ωd/ν，ν为水流运动黏滞系数，见图。

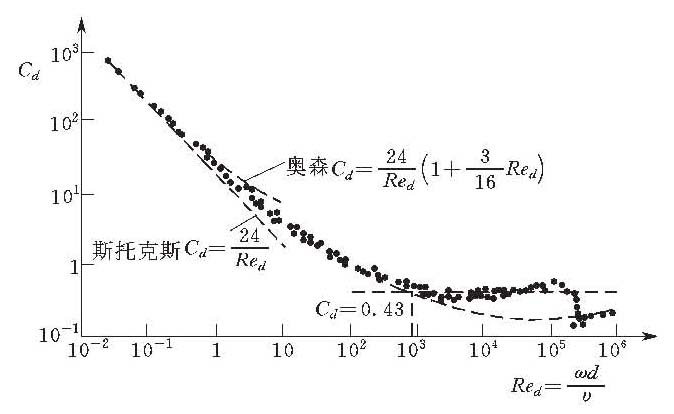
球体沉降阻力系数与雷诺数的关系

（1）雷诺数较小时（Re_d＜0.4）流动为层流，1851年斯托克斯（G.G.Stokes）从理论上求得

式中，μ为水的动力黏滞性系数，由此可得层流情况下阻力系数与雷诺数成反比，将C_d=24/Re_d，代入式（3）后得层流区球体沉速计算公式

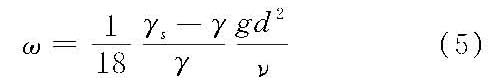
（2）雷诺数较大时（Re_d＞1000）流态为紊流，阻力系数与雷诺数无关，由试验得C_d=0.45，代入式（3）后得紊流区球体沉速计算公式

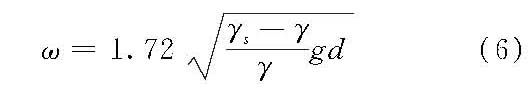
（3）雷诺数Re_d=0.4～1000范围内为过渡区，奥森（C.W.Osen）曾在G.G.斯托克斯解的基础上作了一些改进，推出了阻力系数C_d的理论解，以后不断有人作进一步研究。但迄今为止，所得结果只限于Re_d＜2范围内才与实际资料符合，超出这个范围只能借助于经验或半经验公式。

泥沙颗粒形状很不规则，其沉速与球体沉速应有所不同，计算公式需作一定的修正。实际工作中，在层流区范围内，泥沙颗粒较细，常使用沉速粒径，它是由球体沉速计算公式反推得到的，已包含形状因素影响在内，故可直接使用球体的沉速计算公式。在紊流沉降区，泥沙颗粒较粗，多采用等容粒径或与之相近的筛孔粒径，应考虑形状因素影响，由试验得阻力系数C_d=1.2，代入式（3）后得紊流区泥沙沉速计算公式

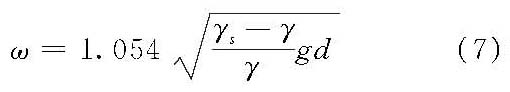
在过渡区也只得使用基于实测资料的经验或半经验公式。